Matematyka i geometria dachu kopertowego

W poprzednim artykule opisałem matematykę więźby dwupołaciowej oraz wielopołaciowej (tzw. koperty) dla przypadku, gdy kąty pochylenia połaci są jednakowe. W tym artykule opiszę zależności dla przypadku, gdy kąty pochylenia połaci są różne.

Rozważania przeprowadzę na podstawie rys. 1.
Z rysunku wynika, że:

1. B1+B2=90°

2. RD1·tgA1=RD2tgA2

3. RD2=RD1·tgA1tgA2=RD1·y

gdzie

y=tgA1tgA2

4. RP2=yRP1

rozstaw płatwi połaci 2

5. RM2=yRM1

rozstaw murłat połaci 2

6. O2=y*O1 (02 – okap połaci 2)

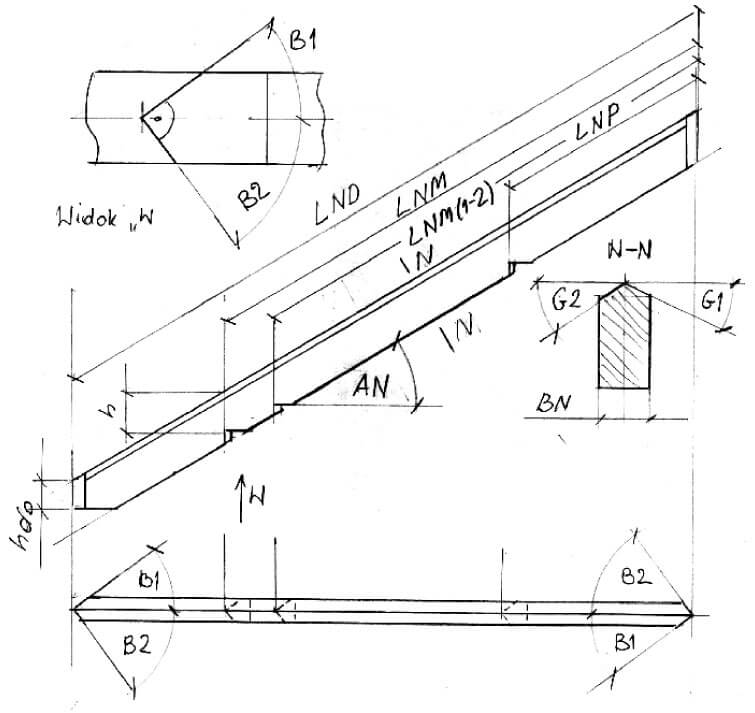
W pierwszej kolejności wyznaczamy wymiary niezbędne do wykonania krokwi narożnej rys. 2.

Mamy:
Kąt pochylenia krokwi narożnej AN

7. AN=arcsintgA1K

gdzie:

8. K=1+y2+(tgA1)2

Wymiary po grzbiecie krokwi odpowiednio do podcięcia pod płatew, murłatę, całej krokwi wynoszą odpowiednio:

9. LNP=K·RP1

10. LNM=K·RM1

11. LND=K·RD1

Wymiary LNM obowiązuje, gdy okap na połaci szczytowej jest zgodny ze wzorem (6). E praktye jednak okap O2 wykonuje się równy okapowi O1. Murłata na połaci 2 zostaje podniesiona o wielkość DHM(1-2) obliczamy ją ze wzoru:

12. DHM(1‐2)=O1·(tgA2-tgA1)-(h2-h1)

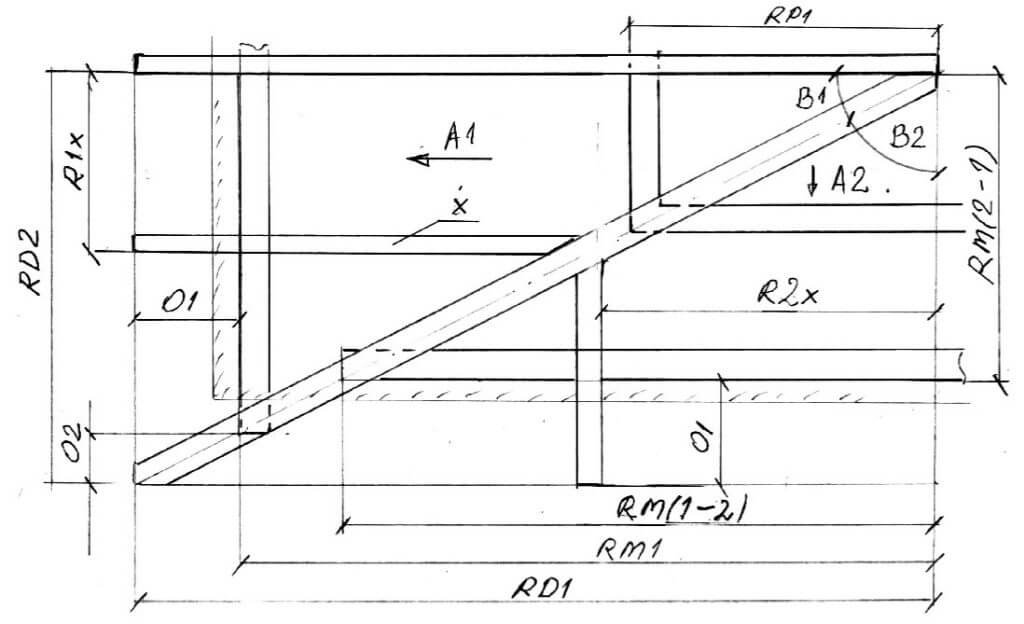
Krokiew narożna oparta jest na narożniku murów w dwóch punktach na wysuniętej murłacie połaci 1 oraz na położonej wyżej murłacie połaci 2.

Wymiary po grzbiecie krokwi do zacięć na murłaty wynoszą odpowiednio:

13. LMN=K·RD1

14. LMN(2‐1)=K·(RD1-O1y)

Schemat tego rozwiązania przedstawia rysunek 3.

Kąty ścięć u wierzchołka krokwi oraz na okapie wynoszą

15. B1=arctgy

16. B2=arctg(1y)=90-B1

Kąty ścięć grzbietu narożnika G1 i G2 obliczamy ze wzorów:

17. G1=90-arccos(sinB1·sinA1)

18. G2=90-arccos(sinB2·sinA2)

Suma kątów G1 i G2 daje kąt przecięcia połaci G(1-2)

19. G(1‐2)=90-arccos(cosA1·cosA2)

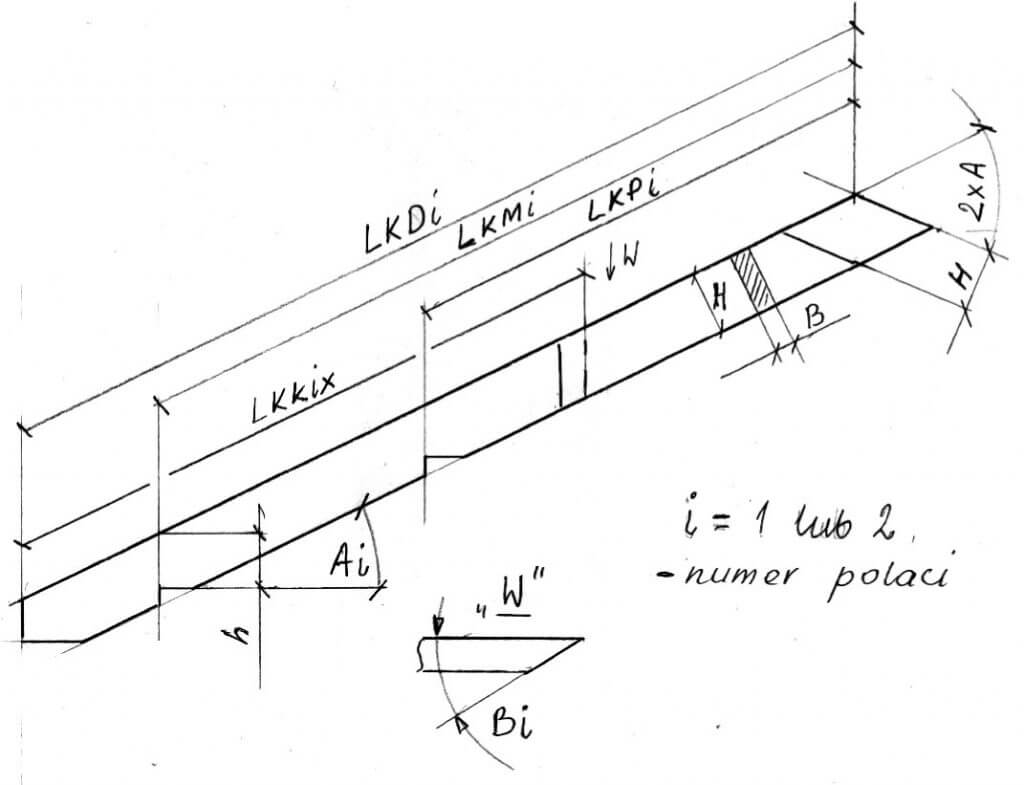
Główne wymiary po grzbiecie krokwi dla połaci 1 wyznaczamy ze wzorów:

20. LKP1=RD1cosA1

21. LKM1=RM1cosA1

22. LKD1=RD1cosA1

dla połaci 2

23. LKP2=RP2cosA2

24. LKM2=RM2cosA2

25. LKM(2‐1)=RD2-O1cosA2

26. LKD2=RD2cosA2

Dla wyznaczania długości krokwi skróconych przydatne są kąty zawarte między krokwią skróconą a krokwią narożną. Wynoszą one odpowiednio:

27. D1=arccos(1K·cosA1)

28. D2=arccos(1K·cosA2)

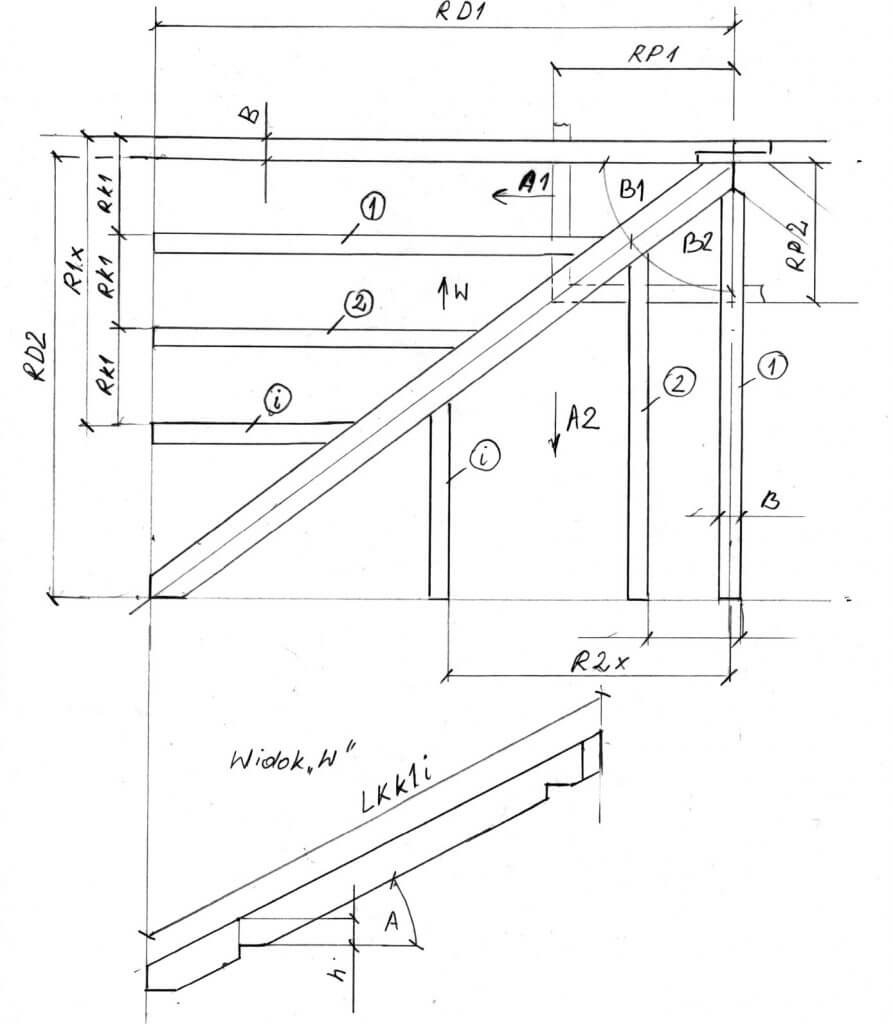
Rozpatrując rysunek 5 można udowodnić, że długość krokwi skróconych dla połaci 1 są odpowiednio:

29. LKk11=LKD1-(RK1-B)·(1tgD1)-dSK1

30. LKk1i=LKk11-(I-1)Rk1·(1tgD1)

gdzie: i-kolejny numer krokwi skróconej

31. dSK1=BN2·1sinB1·cosA1

dla połaci 2

32. LKk21=LKD2-dSK2

33. LKk22=LKk21-(Rk2-B2)·1tgD2

34. LKk2i=LKk22-(I-2)Rk2·1tgD2

gdzie:

35. dSK2=BN2·1sinB2·cosA2

dla krokwi skróconej, której położenie określane jest wymiarem Rx długość określana jest wzorami dla połaci 1

36. LKk1x=RD2-R1xtgD1-dSK1

a dla połaci 2:

36. LKk2x=RD1-R2xtgD2-dSK2

Korekcja długości krokwi na połaci o większym pochyleniu

Ponieważ dla więźb o różnych pochyleniach, gdy różnica między wartościami pochyleń jest znaczna wykończenie okapu deską okapową staje się kłopotliwe. Rozwiązaniem dla tego problemu jest skrócenie krokwi po jej grzbiecie dla połaci o większym A o wielkość dLK jak na rysunku 6.

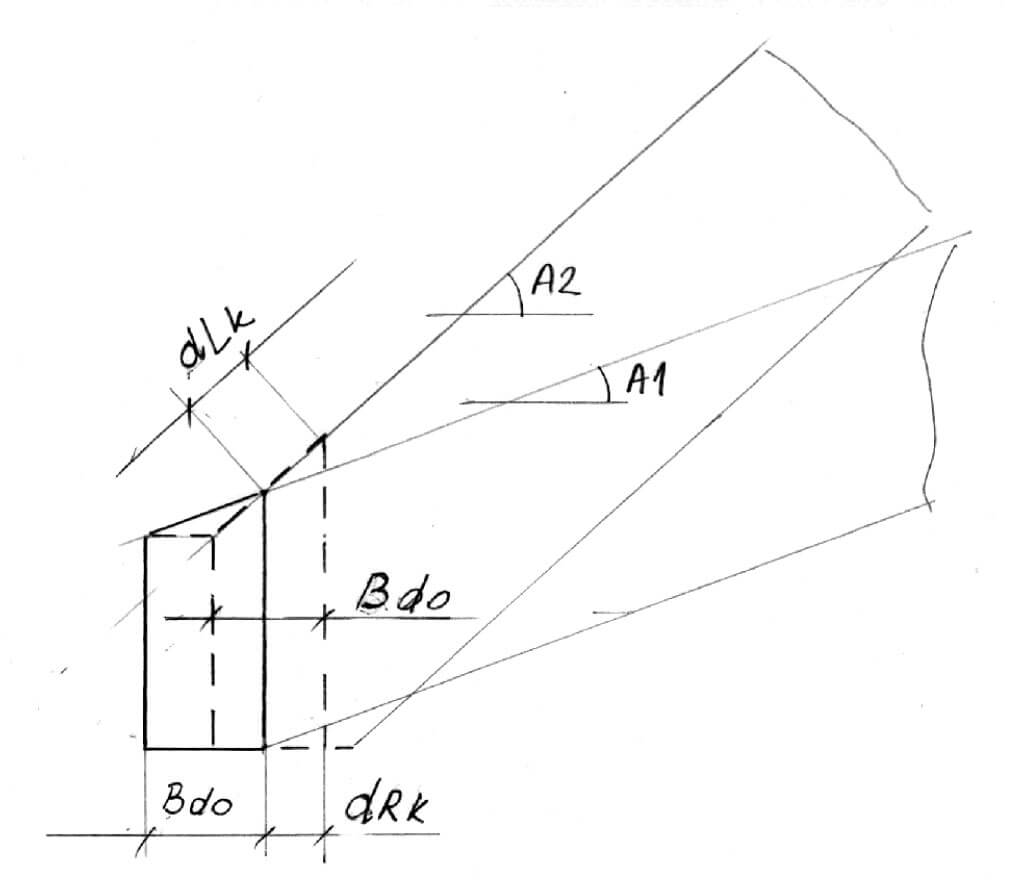
38. dLk=dRkcosA

gdzie

39. dRk=(1-y)·Bdo

Bdo – grubość deski okapowej

Mgr inż. Paweł Jatczak
ZUPH „Wizar”
Usługi ciesielskie